A Waiting Game Part 2

Now comes the fun part! Is it possible to guess the nationality and gender of a person, if I know how long he/she is willing to wait for someone, or make someone wait?

This becomes a simple classification problem in machine learning.

First let’s try modeling the problem using the k-nearest neighbors (KNN) algorithm, which is a non-parametric method meaning that it makes no assumption about the mathematical relation between the input predictors and output response. When given an unknown, the KNN classifier first identifies the K points* that are closest to the unknown, then estimates the conditional probability for each classification. *K points - the exact number of points is determined by the user, and needs to be optimized in order to minimize prediction error. For a much better explanation, see chapter two of ‘An Introduction to Statistical Learning’ by James, Witten, Hastie, and Tibshirani.

Here is the raw data file: JpHWWaittimeDataPublic.csv

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.neighbors import KNeighborsClassifier

# fix data so that they have numerical values for all predictor columns
df =pd.read_csv('JpHWWaittimeDataPublic.csv')
local = []
for index, item in df.iterrows():
    line = item['Nationality']
    result = bool('Japan' in line)
    local.append(result)
df['isJapanese'] = list(local)

gender_score = []
for index, item in df.iterrows():
    line = item['Gender']
    result = bool('Female' in line)  # Female = True = 1
    gender_score.append(result)
df['GenderScore'] = list(gender_score)

df2 = df.drop('Nationality', axis=1).drop('Gender',axis=1)

# to predict whether the subject is Japanese
# first create classifier, and fit the classifier to the data
x = df2.drop('isJapanese',axis=1).drop('GenderScore', axis=1).values
y_isJapanese = df2['isJapanese']

knn = KNeighborsClassifier(n_neighbors=8)
knn.fit(x, y_isJapanese)

y_isJapansese_pred = knn.predict(x)

# check the error rate of the prediction using knn classifier
score_isJapanese = knn.score(x, y_isJapanese)
print('Predicting whether is Japanese score: ', score_isJapanese)
print()

# to predict gender
y_Gender = df2['GenderScore']

knn.fit(x, y_Gender)
y_Gender_pred = knn.predict(x)
score_Gender = knn.score(x, y_Gender)
print('Gender prediction score: ', score_Gender)

Nationality prediction score: 0.676470588235
Gender prediction score: 0.764705882353

We can divide the dataset into training set and test set, so that we can use the accuracy score for the test set to gauge the performance of the classifier in real case scenarios. However, since in this case, the number of subjects is not very many, instead of dividing the dataset into training and test sets, we can use cross validation to see how the classifier should perform in practice:

from sklearn.model_selection import cross_val_score

knn = KNeighborsClassifier(n_neighbors = 8)
isJ_cv_scores = cross_val_score(knn, x, y_isJapanese, cv=4)
print('Predicting whether Japanese: ', isJ_cv_scores)
print('Mean: ', isJ_cv_scores.mean())

Gender_cv_scores = cross_val_score(knn, x, y_Gender, cv=4)
print('Predicting gender: ', Gender_cv_scores)
print('Mean: ', Gender_cv_scores.mean())

Predicting whether Japanese: [ 0.77777778 0.55555556 0.625 0.5 ]
Mean: 0.614583333333
Predicting gender: [ 0.66666667 0.66666667 0.5 0.75 ]
Mean: 0.645833333333

The above is only a very rough first estimate of our ability to predict nationality (Japanese or non-Japanese) and gender. To improve predictive ability, we can try,
1) using the same classifier, knn, but optimizing the number of n_neighbors
2) selecting only the important predictors using lasso regression
3) using derived features
4) switching to a parametric classifier, such as logistic regression

1) Optimizing n_neighbors:

neighbors = np.arange(1, 12)
train_accuracy_isJapanese = np.empty(len(neighbors))

# looping over different numbers of n_neighbors and recording the accuracy with each
for i, k in enumerate(neighbors):
    knn = KNeighborsClassifier(n_neighbors=k)
    knn.fit(x, y_isJapanese)
    train_accuracy_isJapanese[i] = knn.score(x, y_isJapanese)

# visualizing results by plotting accuracy over different values of n_neighbors
plt.title('k-NN: varying the number of n_neighbors')
plt.plot(neighbors, train_accuracy_isJapanese, label = 'isJapanese Training Accuracy', color = 'blue')
plt.legend()
plt.xlabel('Number of n_neighbors')
plt.ylabel('Accuracy')
plt.show()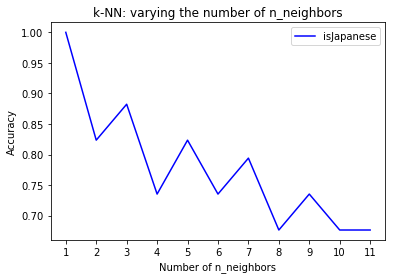

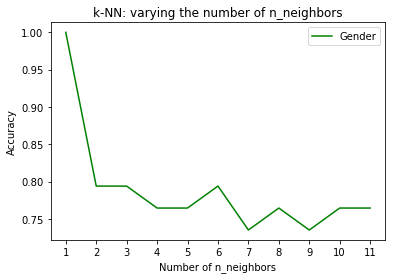
It looks like a n_neighbors = 3 should give better accuracy, and using similar code as the above but n_neighbors = 3, the cross validation accuracy is as follows:

Predicting whether Japanese: [ 0.88888889 0.66666667 0.625 0.5 ]
Mean: 0.670138888889
Predicting gender: [ 0.77777778 0.77777778 0.375 0.625 ]
Mean: 0.638888888889

Changing to n_neighbors=3 helps with predicting whether the test subject is Japanese, however it doesn’t help with increasing accuracy with predicint gender.

Therefore, next I will try including only the features that have the biggest impact on the output. This can be done by using lasso regression:

from sklearn.linear_model import Lasso

names = df2.drop('isJapanese',axis=1).drop('GenderScore', axis=1).columns

lasso = Lasso(alpha=0.1) 
lasso.fit(x,y_isJapanese)
lasso_coef = lasso.coef_

plt.plot(range(len(names)), lasso_coef, color='blue', label='isJapanese')
plt.legend()
plt.title('Lasso regression')
plt.xticks(range(len(names)), names, rotation=60)
plt.ylabel('Coefficients')
plt.show()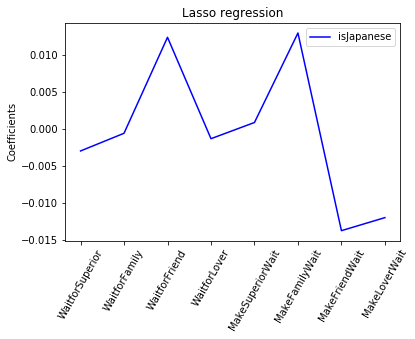

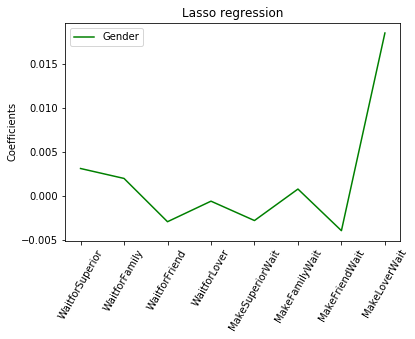
The lasso regression shows that some features definitly contribute more towards the prediction accuracy over other features. So now we include only those features:

x_isJ_selected = df2.loc[:,['WaitforFriend','MakeFamilyWait','MakeFriendWait','MakeLoverWait']]
y_isJapanese = df2['isJapanese']

x_Gender_selected = df2.loc[:,['WaitforSuperior','WaitforFriend','MakeSuperiorWait','MakeFriendWait','MakeLoverWait']]
y_Gender = df2['GenderScore']

Using the knn classifier with n_neighbors = 3, the cross validation accuracy scores are:

Predicting whether Japanese (n=3): [ 0.88888889 0.77777778 0.75 0.625 ]
Mean: 0.760416666667
Predicting Gender (n=3): [ 0.77777778 0.77777778 0.625 0.625 ]
Mean: 0.701388888889

The accuracies are getting better. Next time we shall see if adding derived features and switching to logistic regression will further improve accuracy.